|
Size of the Universe Part 3 The subject matter of this page is probably more my cup of tea than the first two pages. Still, I had forgotten a few things and consulted a few astrophysicist types about a couple points regarding relativity, but they were about as helpful as an umbrella in a hurricane. I must thank Mr. Seligman, though, for his help with orbital mechanics. As for references for this page, I have a book titled “The Unexpected Vista” 1983 by James Trefil that was particularly helpful with its numerous simplistic diagrams. And I think the old World Book encyclopedia article on special relativity is hard to beat. As for the Internet: Wikipedia is often helpful, but the problem is, if there are any webpages with the following information in them, the information is usually presented in such a complex and esoteric way, that there are few I can specifically recommend for the non-scientist. The Coriolus Force (and Effect) and its
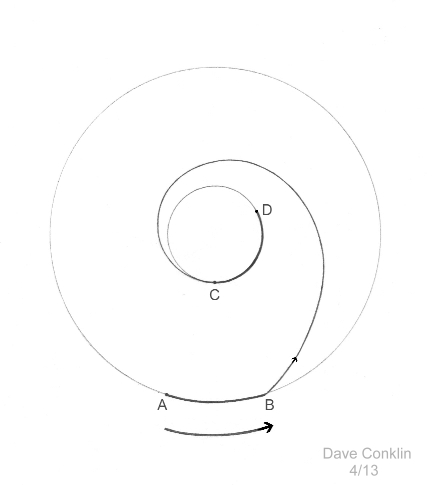
Relationship to Orbital Mechanics At the heart of the Coriolus force is the fact that when any object traveling in an arc is pulled into a tighter arc, the object not only wants to travel the same distance over a given amount of time—a tendency commonly referred to as inertia—but also gains speed (tangential velocity) as the pulling force is transferred to it. Under certain circumstances, like living on the surface of a large rotating planet, this might be perceived as a new force acting on an object—the Coriolus force—when the object is propelled in a north or south direction. A measurable quantity of the object’s mass and speed-relative-to-another-object is the object’s momentum, or angular momentum in the case of rotating objects. Smaller circles with tighter arcs have a smaller circumference, of course, so any object traveling a tighter arc will need to make more revolutions to cover the same distance as it would traveling a greater arc. If the objects being forced to travel a tighter arc happen to be a skater’s appendages, the momentum of those appendeges will be transferred to his or her entire body, which, of course, will spin faster, i.e., turn more revolutions over a given amount of time, his or her angular velocity increases. Imagine a female skater going into a spin. A skater is a closed system, so we can’t say the skater gains momentum when she pulls in her arms, as momentum can only be transferred from somewhere else. But an interesting question might be, does any part of her actually move faster after going into a tight spin than her fastest moving parts were moving before tightening her spin? In other words, does the skater’s fastest tangential velocity actually increase? tangential velocity being the rotational equivalent of linear velocity. Prior to tightening her spin, her fingertips and toes on one foot are her fastest moving parts. After tightening her spin, either her shoulders or her hips are her fastest moving parts depending on her arm position. Whatever the ratio might turn out to be for one skater, it would not apply to every skater, of course, as each skater would have a slightly different mass distribution. Skaters must exert energy to bring in their arms. This energy might add to the momentum of her arms if it were not for the fact that, as we have already determined, some of that momentum from her arms is in turn transferred to her middle. Also, in a skater’s case, there is friction with the ice, and wind resistance, to deal with. As a result, my best guess is that if her widest parts are moving any faster than her fingertips did before she pulled them in, it’s probably not by much. But now let’s imagine a setup where we can recreate what the skater does without the friction, wind resistance, or mass of the skater’s body. Imagine a round platform about the size of a merry-go-round sitting in a large vacuum chamber. At the center of the platform is a hollow pole. At the top of this pole is a frictionless swivel with a pulley mounted on it that has very little mass. Lying on the edge of the platform is a spherical weight. A tether with a very high strength-to-mass ratio runs from the weight through the pulley and down through the pole to a remote-controlled electric winch. The pole and winch are firmly mounted to the Earth. The entire platform begins to spin in a counter-clockwise direction and accelerates until the spherical weight lifts off the platform. At this point, the platform stops spinning any faster, and the edge of the platform and the weight are both moving at the same steady speed. The winch is activated, and the weight is drawn inward towards the pole. The tether never twists due to a frictionless swivel where it fastens to the weight. The closer the weight gets to the pole, the more revolutions the weight will make, of course, over X amount of time, and the winch will have to pull ever harder on the tether. But now, unlike the skater, none of the energy transferred to the weight through the wire gets lost to friction or wind resistance. And very little of the weight’s momentum gets transferred to the pulley or tether because of their low mass, so the weight does move considerably faster the closer it gets to the pole as the work done by the winch adds to the weight’s momentum.
Side note: In physics, the tension on the tether is typically measured as centripetal force. I am not sure I agree with this. When the weight is being pulled in, I would argue that there are three forces working on the tether, with one being the steadily increasing force needed to pull the weight in. But after that, when the weight is orbiting at a set distance, I would argue there are two opposing forces at work on the wire; one being a centripetal force provided by the super-strong molecular bonds of the tether, and the other being a centrifugal force caused by the inertia of the weight. So in my opinion, the tension on the tether is an outward force that should be measured as centrifugal force, but then, I didn’t make up the rules. Now imagine the above apparatus/diagram represents the Earth looking down from high above the North Pole. It would be as if an object were forced from the equator all the way to the Arctic Circle. Of course, in the real world, I don’t think there are any jet streams that typically travel all the way from the equator to Arctic Circle, but even if one did—like the spinning skater—even channels of wind lose energy due to friction with the surrounding air, resulting in a transfer of momentum and, no doubt, a tiny loss of energy in the form of heat. But the diagram does show why the Corilolus force is such a factor affecting Earth’s weather. But now let’s make gravity the centripetal force. Gravity could never do what the tether did, of course. Gravity is not anywhere close to being that powerful, and the force of gravity cannot simply latch on to an orbiting object, increase in strength, and reel in an object. What’s different about an object held in orbit by a balance between gravitational attraction and its own momentum is that the object will need to first lose momentum in order to achieve a lower orbit. As the object falls, it is, of course, accelerated by the pull of gravity. In doing so, it gains kinetic energy and therefore momentum. But it will gain too much speed to maintain a circular orbit, and will naturally take on an elliptical orbit. As it then rises and slows to apoapsis, it loses kinetic energy and momentum, and gains potential energy. In the case of a spaceship, a subsequent forward burn at periapsis will slow the ship into a more circular orbit, where, although its speed will not be anything like the 11.11 times faster speed of the weight, it will be moving faster than its original orbit. This can lead to some really counterintuitive stuff when trying to grasp orbital mechanics: An orbiting space ship must first put on the breaks to fall and subsequently be accelerated by the force of gravity into a lower orbit, where it will not only make more orbits in X amount of time, it will also acquire a higher average velocity. And to achieve a higher orbit, it must step on the gas, after which it will rise upwards and slow down, where it will not only make fewer orbits per X amount of time, but move at a slower average velocity as well. To summarize: When a force is applied to an object that causes the object to follow a tighter arc, the force will add to the objects momentum unless that energy is somehow directed elsewhere. Any object moving across the Earth’s surface in a north or south direction will experience a deflection due to conservation of angular momentum. In the northern hemisphere, the deflection will be to the east (in the direction of Earth’s spin) for any object moving north, and the deflection—although to a much lesser degree—will be to the west for any object moving south. However, in the everyday scheme of things, this deflection is hardly noticeable due to the Earth’s relatively slow speed of revolution and the fact that the Earth is round. It is enough, however, to affect a broad northerly or southerly wind.
Special Relativity As Einstein pointed out through his theory of special relativity and in his famous equation, sub-atomic particles are always in motion, even inside the atom; so it is a bit unsettling to ascribe a location where something that is always in motion can be described as being at rest. However, there is a theoretical point in empty space where any atom or object residing there could be said to be motionless—a point where time runs the quickest, and the object could be said to have zero velocity. By “empty space,” I am referring to a section of empty space far removed from any galaxy, where any influence from the gravitational fields of other objects is negligible. Any light pulse passing through such space would travel in a perfectly straight line and also travel faster than any light wave that happened to be propagating near clumps of matter, yet it would still be traveling at exactly 186,282mps, if you catch the drift. And a second object in a similar patch of empty space a thousand light years away would be stationary relative to the first (except for the gradual expansion of space). The closer one gets to a gravitational field, however, the more this concept breaks down, as—if I understand anything about gravity—this theoretical point becomes a line extending away from the atom opposite the source of the field. The objective of creating these pages was to put some of science’s most esoteric theories in simplistic terms without using a lot of big words, math equations and historic details, so I hate to get into another history lesson like every other article that’s been written on relativity, but I feel I must to go any further. If you have studied particle physics at all, then you must be aware of the pivotal moment in the study of light when Albert Michelson and Edward Morley carried out their light measuring experiments in 1887. I have something like nine or ten books on physics, and between those and other sources like the Internet, encyclopedias etc., all seem to have a slightly different take on the experiments. At the time Michelson carried out his experiments, what we now call space was commonly referred to as the luminiferous aether. This “ether” was viewed as a sort of perfect medium, never bending or stretching (except to accommodate a light wave); something separate from solid matter. And the concept of time running at a different pace for two observers never crossed anyone’s mind. Michelson set out find the Earth’s direction of motion through the ether. I have one old book from the 1960s that describes Michelson as expecting light to get a boost from the motion of the earth much like a baseball thrown from the front of moving train. Another more up-to-date one simply relates how he expected light to travel faster opposite the Earth’s motion. While neither is entirely inaccurate, both are probably equally bad at explaining things. The experiment involved a beam of light that was split up, with the two subsequent beams traveling at right angles to each other until they were reflected back to their starting point by two equidistant mirrors. The to-and-back method was used because one-way measurements performed on the surface of the Earth are impractical. He expected one of the beams to take slightly longer than the other; specifically, the beam that happened to be pointed in the direction of, or opposite of, the Earth’s direction of travel. According to the logic of the time, as the Earth traveled around the Sun, its velocity through the ether should have been affecting a slight change in speed of light as measured on the Earth, which should have shown up as a greater discrepancy between the two beams the faster this relative velocity was. The discrepancy should have shown up as interference patterns between the two beams. However, regardless of how many times he checked it, no such interference patterns showed up; the speed of light always came out the same. It was this very finding that would eventually lead Einstein to his theories on the subject of relativity. The following diagram is what Michelson would have expected to see if he had performed his light experiment on a spaceship traveling at 6/10 the speed of light—before his famous experiment. The left side of the diagram represents Michelson’s apparatus and what Michelson would have expected a person (Observer A) moving along with the apparatus to see. The right side of the diagram is what Michelson would have expected the experiment to have looked like to a person (Observer B) watching the space ship go by. Imagine that prior to the experiment, two probes containing mirrors were launched from the spaceship, one in the direction of the ship’s travel and one at a right angle, both stopping at a distance of 1 million miles; effectively making his experiment apparatus 1 million miles long and 1 million miles wide. For illustrative purposes, I have slowed the speed of light to precisely 166,666.66mps. |

This diagram is what Observer A would actually see.
Like the results of Michelson's actual experiment, to Observer A, it
would have
appeared as if the space ship was completely motionless. Keep in mind
that this entire exercise is strictly for a coasting spaceship, not an
accelerating or decelerating one. |
|
The following diagram explains why according to Einstein’s
special theory of relativity: Observer B would actually see something
different than Observer A.
But even before Einstein came up with his theory, scientists were
attempting to explain the results of the Michelson-Morley experiment. A
result of these attempts was a math formula called the Lorentz
transformation, which used both length contraction and a slowing of
time (time dilation) to explain the results. It is the fundamental
aspect of special relativity. |

|
As you can see, Michelson’s apparatus would have actually contracted by
20% along the ship’s direction of travel. His clock would also have
been running 20% slower than anyone at rest (i.e., Observer B). Hence,
both his right-angle light beam and his direction-of-travel light beam
would have traveled to and back in 12 seconds. Micheson would not have
been aware of his circumstances; he would still have perceived his
apparatus to be 1 million miles long in his direction of travel, so his
speed calculation for both light beams would have equaled
166,666.66mps; exactly the same figure arrived at by Observer B, who
can see the entire distances travelled by the two light beams. A link for those like myself, who would rather get a tooth pulled than look at a square root symbol: Time dilation/length contraction But what would happen if someone in such a hypothetical position attempted to measure their direction-of-travel light beam in only one direction? Imagine now that observer A launches another probe in his direction of travel. This time, the probe has a clock aboard that was synchronized with the ship’s clock before it was launched. The probe travels away from observer A's ship very slowly (in comparison to the speed of light) until reaching a distance of one million miles—according to Observer A’s ruler. Measuring the speed of light at 166,666.66mps, observer A expects light to travel back from the probe in 6 seconds. Light actually travels back in 2.4 seconds, but when he looks through his telescope at the clock, it is 6 seconds behind—just as he expected. Here is why: Say, from Observer B’s perspective, he sees the probe travel to its destination at an average speed of 300,000mph faster than Observer A’s ship. He would watch the gap between the ship and probe widen for 160 minutes until it was 800,000 miles long. The ship would cover a lot of distance, of course, in 160 minutes; and its clock at that very time would read 128 minutes, or 0.8 of 160. Due to the probe’s slightly faster velocity (.6005c), the clock aboard the probe runs slower than the ship’s, giving it a time dilation of about 0.799625. That adds 3.6 seconds of time dilation to the probe. In other words, the probe’s clock would read 127 minutes 56.4 seconds. Now, remember that 2.4 seconds of Observer A’s time that it took for the clock image to travel back? By the time that clock image reading 127 minutes 56.4 seconds gets back to the ship, the ship’s clock reads 128 minutes 2.4 seconds, a difference of 6 seconds. Using space as a reference frame still remains elusive. As mentioned, at the time of Michelson’s experiment, light and the medium it traveled upon (the ether) were still looked upon as something separate from matter. This posed a constant dilemma with regards to just how matter managed to travel through the ether at all. But drawing—either directly or indirectly—upon theories such as the one put forth by Maxwell in 1864 that light might be electromagnetic in nature, the results of Michelson’s experiment in 1887, the discovery by Hertz in 1887 that certain metals give up electrons when exposed to ultraviolet light, and the Lorentz transformation, Einstein theorized that matter, mass, space, energy and time were much more closely intertwined than anyone had previously realized; in other words, light was matter and matter was light—all vibrations of the same medium. But with that said, I think I’m safe in saying that others, including Hendrik Lorentz, were beginning to think along pretty much the same lines as Einstein by 1905, and did not view the ether in quite the same way as they might have in the past. I am not sure if I fully understand why Einstein’s theory was so “special,” but I believe it is in the idea that in the everyday scheme of things, the universe could still be viewed in the old Galilean tradition of relativity—that an object's position or velocity can only be judged in relation to other objects. Therefore, using the ether as a reference point, or including it in any equation regarding a particle's position, velocity, or time frame, was pointless. Later, in his general theory of relativity, Einstein further eroded the concept of the ether by describing a medium that could be curved or stretched in the presence of matter. Einstein simply referred to this medium as “space.” On the Nature of Space Time Dilation and the Two Clocks |
|
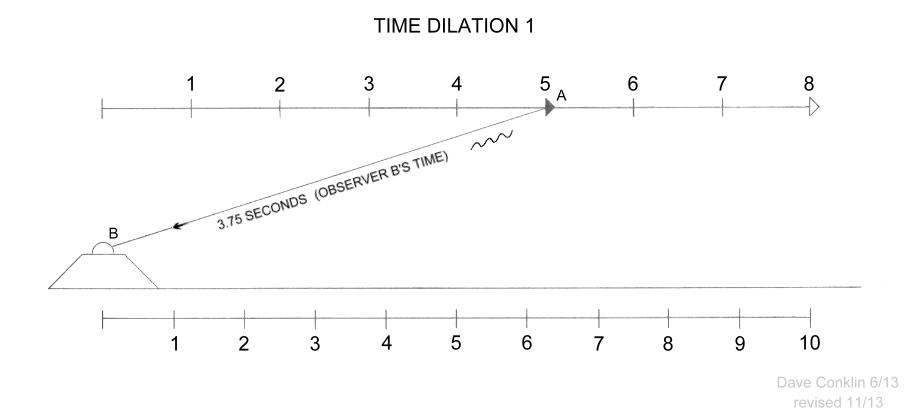
In this next diagram, at 8 seconds on his clock, Observer A
records an image through his telescope of Observer B’s observatory. Of
course, observer A does not realize he is the one truly in motion.
En route to the outpost, he measured the speed of light and came to
the conclusion that he is the truly stationary one. Believing the
observatory has passed him at 0.6c, he expects Observer B’s stopwatch
to read 5 seconds, allowing 3 seconds for the light to have traveled
back. Instead, it reads 4 seconds; again, 20% slower than his
prediction. The light has actually traveled for 4.8 seconds, starting
out when his spaceship was 3.2 seconds from the tower. |
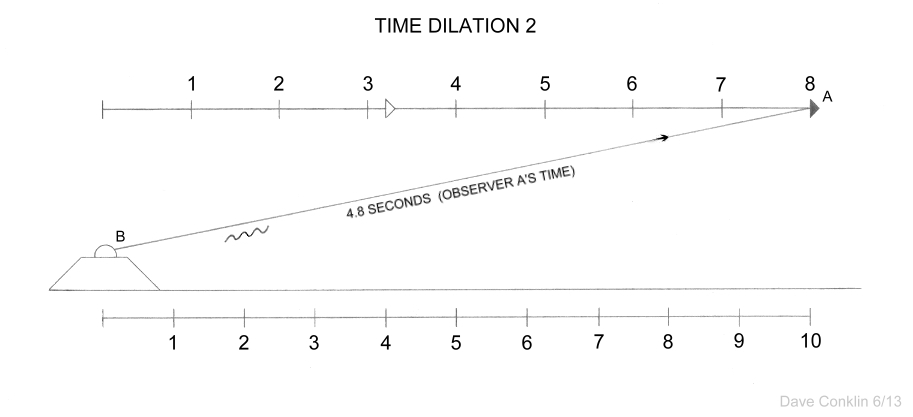
|
But here is the thing: For the two-clock scenario to work, Observer A has to be ignorant of the fact that he is the one who is truly in motion. But the fact is, for an observer like Observer A, who is moving at such an extreme velocity, there would be things that would likely tip you off. If I understand correctly, the interior of the spaceship would appear the same; however, starlight coming from the galaxies in the ship’s direction of travel would be drastically blue-shifted, and starlight from the opposite direction, red-shifted. To summarize: Einstein was attempting to unify a number of experimental results and theories with his special theory of relativity. Relativity does not deny the existence of a medium, it only points out its uselessness as a frame of reference. Vaguely similar to the concept of the ether, there is a universal state of motionlessness for any atom or object sufficiently off by itself, however useless it might be as a frame of reference. |
SIZE OF THE UNIVERSE PART 4
BACK TO SIZE OF THE UNIVERSE PART 2
HOME
mysteries, commentary, sci-fi