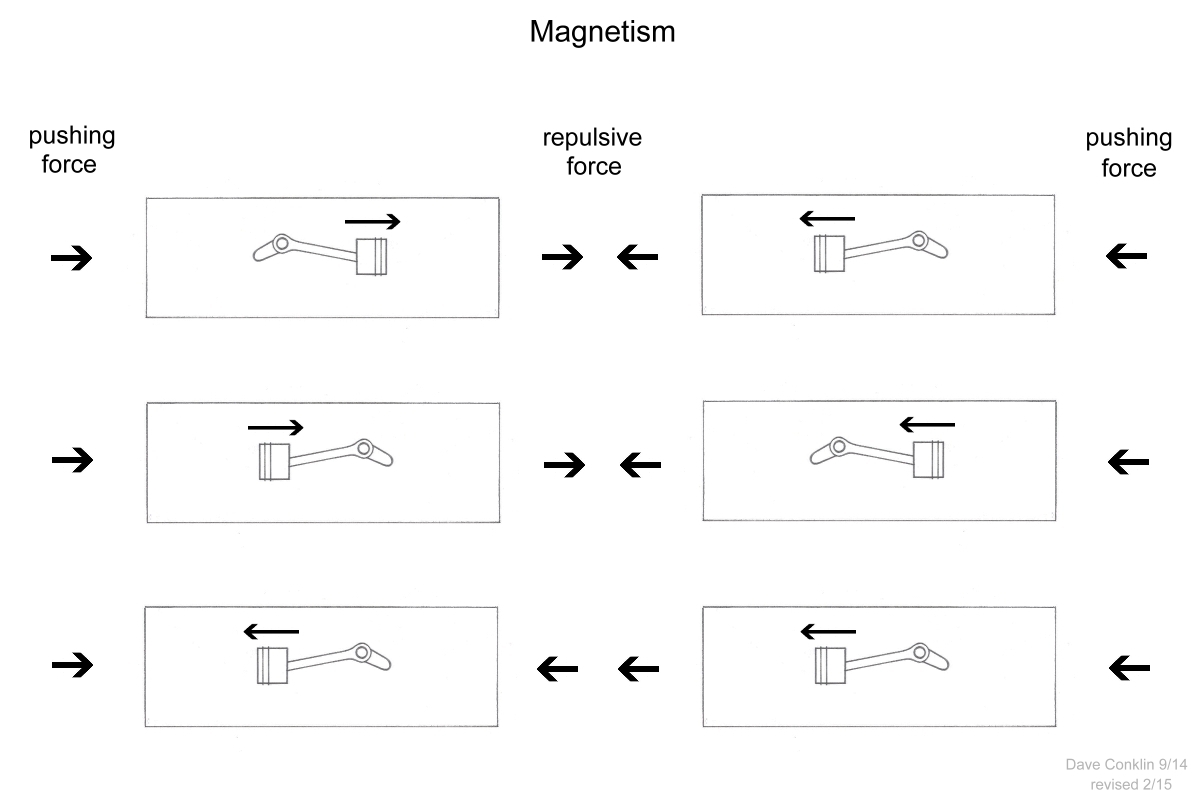
Size of the Universe Part 4

Dave Takes On Electromagnetism

[Note: This page became very long, so I decided to trim the fat into something more readable, and separate it from my ideas on gravity.]

A while back, I did an Internet search for “how magnetism works.” Guess what turned up—absolutely nothing. One page I came across went into great lengthy detail describing a magnetic field from a purely mathematical perspective; didn’t stay long. Interestingly, I came across a few remarks in the comments sections of a couple web pages that were echoing my own sentiments, comments to the effect: “Why can’t any of these scientists, if they are so smart, explain how magnetism works.” I concur. Here we are, more than 150 years after Maxwell's field equations, yet I have never heard any sort of clear explanation of what charge is, or why magnets or charges repell or attract. So I put this page together as a challenge, I suppose, to the status quo, under the notion that if something is so incredably hard to explain, there must be something wrong with the concept.

I want to stress that this particular page should not be taken as anything academic. It is entirely hypothetical and based on my own ideas of how nature might do what it does; and is completely at odds with the current way of looking at both magnetism and gravity, which is to imagine both as more or less static phenomena, in the sense that neither involve any motion or oscillating quality. (rev 2/26/19, 10/08/20, 10/28/20)

The heart of magnetism is, of course, the humble electron, a negatively charged particle. But what is charge? I think something called phase has a lot to do with it. When you hook two stereo speakers up correctly, you get nice loud bass. When you hook one up backwards, suddenly, your awesome sounding stereo system sounds wimpy. One speaker is moving in while the other is moving out. So you crank the bass knob up to 10, trying to hear some low-end until thppppp—time for some new speakers. I believe charge works in much the same way. While neutrons and uncharged atoms exist in a more-or-less phase-cancelled state, much like the miswired speakers in our stereo example, charged atoms are a different story: Electrons are always oscillating in one direction, let’s say outward, while protons are oscillating inward. So add or subtract an electron from a neutral atom, and the "stereo" comes alive. Oscillating inward and outward from where, you might ask? Well, that’s a good question. Inward and outward from another dimension is my only answer.

So you might view the electric field surrounding a collection of charged atoms as something like a beach ball inflating and deflating, al-be-it a beach ball with no defined surface. That positive charge under the oak tree in your yard is puffing outward while that negative charge up in the cloud is puffing inward. And when that positive charge under the oak tree in your yard is puffing inward, that negative charge up in the cloud is puffing outward, growing in strength, until . . . (rev 6/28/19)

It is important to keep in mind, here, that these oscillating pulses, which I prefer to call them, do not travel outward like a sound wave or wave across water. In this case, the entity we call space simply compresses and springs back in what you might call a reflex action. I am going to assume that the influence of these in-and-out pulses on other charged atoms—in other words, the back-and-forth motion of space between two charges—is instantaneous regardless of distance, with the strength of that influence falling off in accordance with the inverse square law (unless aided by a conductor). This seemingly defies Einstein’s assertion that nothing can travel faster than the speed of light, but to assign a speed to such pulses suggests a propagating wave, which I don’t believe is the case. Electromagnetic waves—photons, if you will—obviously do, on the other hand, keep traveling outwards until running into something, and their speed cannot exceed the speed of light.

Like the opposite poles of a magnet, opposite charges attract. But when it comes to charges building up, the electrons tend to break free before there is any great tug between the atoms themselves.

Now magnetism: Electrons orbit the iron atoms in a magnet crossways the magnet. In other words, they orbit at a right angle to N and S. With each in/out pulse of the electrons/protons in the atoms, there is a corresponding pulse at a right angle to the electron’s orbit. The direction of the pulse alternates between the north and south poles of the magnet.

But whereas the in/out pulses of an electric field around a charge are normally spherical in nature, the back-and-forth sideways pulses of a magnetic field are capable of aligning themselves in ferrous materials. Get the orbits of enough electrons lined up, and a powerful force is created—magnetism.

I believe I am correct in stating that an ordinary magnet does not possess an inherent electric charge, therefore it is interesting to note that while the in and out motion of the electrons are normally phase cancelled in the atoms of a magnet, the opposite is true for the sideways motions.

I like to visualize the pulses that produce magnetism as a piston moving back and forth from north to south, south to north. Now imagine a second magnet—a second piston moving back and forth in perfect sync with the first. Call the top of each piston north if you would like. Position the pistons (magnets) so that north is facing north. Notice that once every stroke, the pistons are moving towards each other—repulsion. Turn both pistons around so south is facing south; still, once every stroke, the pistons will be moving towards each other. But now, only turn one piston around so that south is facing north. The pistons move in tandem; there is no repulsion, and any force then wishing to push the pistons together can step in and do its thing.

As mentioned, electromagnetic waves travel outward at or near the speed of light, and as any grade-school science book will probably tell you, light waves are transverse waves, with not only an up and down component, but a sideways component as well. So what I refer to as pulses could, for visualization purposes anyhow, be looked at as products of the actual wave, much like a small boat rising and falling as the wake of another boat passes underneath. Or you could look at it as the water itself in a particular spot rising up and down as the wave energy passes through—whatever works. 

One thing I think is misleading is the typical way a light wave is illustrated—as a long spaghetti string of successive waves (even I am guilty). I think if you could actually freeze a photon in time, it would be a single wave—a bump (a motion of space) rising up or down with a corresponding sideways motion. Even if I am wrong regarding photons, the spaghetti string idea certainly could not be applied to electrons, or you could not get the back and forth motion needed to produce such defined vibrational fields.

Another typical illustration is the old series-of-ripples-on-a-pond idea used to depict electromagnetic waves emanating from a radio tower, spreading out and dissipating over time. This is a correct depiction, and the amplitude of such waves can vary from weak to strong, but you have to remember that the ripples are composed of individual photons, which themselves do not do not spread out and dissipate in such a 360-degree manner, have very little curve along their leading edge--if I understand correctly--and possess a quantified energy level, or amplitude, that is set by their frequency. However, a photon will indeed widen upon traversing long distances of interstellar space. In other words, the stretching effect of universal expansion affects a photon along its direction of travel and at right angles to that direction. (rev 3/26/19)

If any of this makes sense to you, I should point out that this way of looking at things demands that magnetism and electric charges have an inherent frequency. However, I did a search once for the “frequency of magnetism” and was astounded to find absolutely zilch. In fact, I found pages describing the opposite—that an ordinary magnetic field has no frequency. Not only does this contradict everything I thought I understood about magnetism, common sense would dictate that what we call a magnetic field is a vibrational pattern, as evident by the lines of flux that show up in the old iron-filings-over-cardboard example. So there you go: Either I'm crazy or maybe its no wonder that no one can explain how magnetism works. (rev 8/05/19)

Electric power through a conductor:

So as we have established (as science did long ago) an electric field and a magnetic field are both perpendicular components of a traveling electromagnetic wave. So where magnetism can be looked at as a directional concentration of the sideways motions of a group of electrons, an electrical discharge or the flow of current down a wire from a negative charge to a positive charge can be looked at as a flow of electrons facilitated by the directional concentration of the up and down (in and out) motions of a group of electrons. As the pulses in the wire move back and forth from negative to positive, the electrons flow in one direction, creating a dilute magnetic field. A magnet wrapped by a wire can produce traveling waves, of course, in the wire when the magnetic field is jogged. 

If you want to visualize the magnetic field across a wire, simply lay a bar magnet across a wire. The polarity of the magnetic field will depend on which end of the wire is negative and which end is positive. Even better, imagine that there is now a hole drilled through the magnet through its width, and the wire is threaded through it. Now pull the wire taught and spin the magnet around the wire.

Going back for a moment to the first example—of simply laying a bar magnet across a wire—imagine a second wire running parallel to the first. Electron flow in the second wire is the same direction, so lay a bar magnet across the wire positioned so the polarity is in the same direction as the first magnet. Opposite poles of each magnet will, of course, be facing one another, and the magnets (wires) will attract.

So how does this all work, you might ask, if the magnetic fields of both wires are constantly spinning? The trick here is to spin the magnets in perfect tandem. Whenever the magnets line up, the opposite poles will always be pointing towards one another; the wires attract. And yes, no matter what you want to believe is spinning—a static entity or an oscillation—the idea of electrons that all spin in unison, regardless of their point of origin, is a very bizarre concept.

So why would a magnet then interact with a DC current carrying wire, you might ponder? Answer: because the electrons in a magnet are also spinning as they orbit the nucleus of the iron atoms. That is a very convoluted thing to visualize, indeed, but in the context of my diagram, you can imagine the "pistons" in each magnet to be rotating in unison, oppositely for the first two sets, the same direction for the last set. (added 3/01/19)

5/19/16: What agrees with my theory:

1 The proven phenomenon of quantum entanglement, which suggests there can be bizarre instantaneous links between matter over great distances.

2 Experiments that have been conducted since James Maxwell formulated his theory on electromagnetism that show all sub-atomic particles have a wave nature to them.

What disagrees, conceptually speaking:

James Maxwell’s electromagnetic theory, apparently: While most every other discovery in physics has been reduced to some understandable form that goes beyond a set of esoteric math equations; from what I have discovered, the subject tends to be one of the most overlooked areas of physics when it comes to “Maxwell’s Field Equations for Dummies.”

I have tried to digest Maxwell’s papers and equations myself, but so far have not gotten very far. But based on other’s interpretation: One day, while taking into account the measured magnitudes of electric and magnetic attraction, and using a calculation previously used for sound waves, Maxwell arrived at the speed of light. Maxwell also considered a light wave to be something different from an “ordinary” field around a magnet, apparently viewing the magnetic field around a magnet as something static, having no oscillation—an “apparition” that showed itself in the presence of moving electrons. On the other hand, he considered magnetic waves to be oscillations of the same apparition. One Wikipedia article I came across states that his theory considered any “action at a distance” to be something that only goes on inside a magnet’s own field. Well, a magnetic field can be channeled, perhaps, but would still not have a defined edge, so exactly where should such action cease, I have to ask? (rev 2/26/19)

Beyond the sources below, I have only found a few brief articles here and there that say pretty much the same thing.

Action at a distance - Wikipedia

James Clerk Maxwell - Wikipedia

History of electromagnetic theory - Wikipedia

2 Einstein’s theory of special relativity: Being somewhat familiar with Einstein’s theories and the man, I believe I am safe in stating that Albert Einstein, like many scientists that came before, did not especially like the idea of any instantaneous action at a distance. So in that sense, anyway, my theory on magnetism conflicts with special relativity.

11/04/16: So according to my theory, which I have dubbed “electric and magnetic fields as oscillations” theory for lack of something better, the electrons and protons responsible for electric and magnetic fields are oscillating in unison, with electrons and protons being in opposite phase. So I put together a couple predictions in regards to my theory:

#1 The oscillations of all electrons are in sync like a single vibration, broken and separated in three-dimensional space. The same applies to protons, with the exception of being 180 degrees out of phase.

#2 The frequency of electromagnetic oscillations must vary depending on the frame of reference. In other words, if one found themselves in a gravitational field stronger than earth’s, or they happened to be moving at an extreme velocity, the frequency of the oscillations would be higher because time would be running slower.

12/07/18: Back when I first Googled “frequency of magnetism;” because my idea of magnetism differed from the status quo, I probably should have Googled “frequency of an electron.” But even then, I wouldn’t have gotten anywhere. Before creating this page, I could remember reading somewhere that the frequency of an electron increases the faster it travels, which only makes sense: If you speed a wave up and then measure it’s frequency, it’s frequency would naturally measure higher, something like the Doppler effect. But while the formulas I found online regarding electron wavelength looked simple enough, at first glance, I found them to be way over my head. In the end, I found no simple table or equation for calculating an electrons’ frequency for a given velocity, with the speed of light being the most obvious reference point. 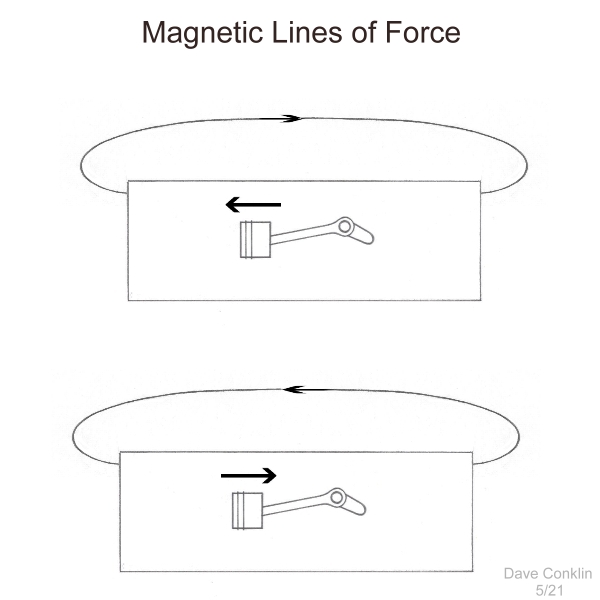So I contacted some of the (supposedly) smartest people in particle physics to see if they could verify my understanding, including David Greene and Fermilab’s “ask a particle physicist.” I got no reply from anyone.

To summarize: I think there might actually be a fundamental zero-velocity frequency associated with an electron, my “frequency of magnetism.” Just don’t ask me what it is.

5/01/21: I thought I could go a little further in explaining the lines of force surrounding a magnet—in the context of my hypothesis. Essentially, the lines of force surrounding a common magnet can be looked at as an oscillating feedback loop, although of a different nature than the annoying squeal from a PA system. I think a cat chasing its tail, first one way, then the other, is a good analogy, as the image doesn’t involve any traveling wave (the cat simply moves its entire body one direction and then reverses course). Another way to describe the phenomena, of course, is the cumulative effect of many, many electron-size feedback loops being squeezed beyond the physical perimeters of the magnet.

1/19/24: Magnetic monopoles

I keep reading again and again about scientists searching for a mythic dragon called the magnetic monopole. Well, in the context of my ideas of what magnetism is, anyway, an electric field is a magnetic monopole. So why doesn’t one pole of an ordinary magnet attract an electric charge, while the other pole repels it, you might ask? Well, this can easily be explained if you do not assume that the back and forth pulses of the electrons in an ordinary magnetic are in perfect sync with their rotation. Therefore, while the pulses may be in sync with all the other electrons in the magnet, and the electrons of any other ordinary magnet, they of a more random nature—in any particular direction—than a perfect “sine wave,” and therefore do not appear to interact with electric fields, which are a perfect sine wave/pulse. So in this context, my diagrams of a back-and-forth piston analogy do not quite tell the whole story.